如何設計更加耐用的3D打印零部件(一)(2)
承載結構的最佳幾何形狀
若要針對專題中每個功能性零件解方程式就有點超過了:況且在日常生活中,又不是所有東西都像橫木一樣重要,但上述理論強調幾個多用途的設計策略,讓我們做出各種形狀的堅固耐用零件。
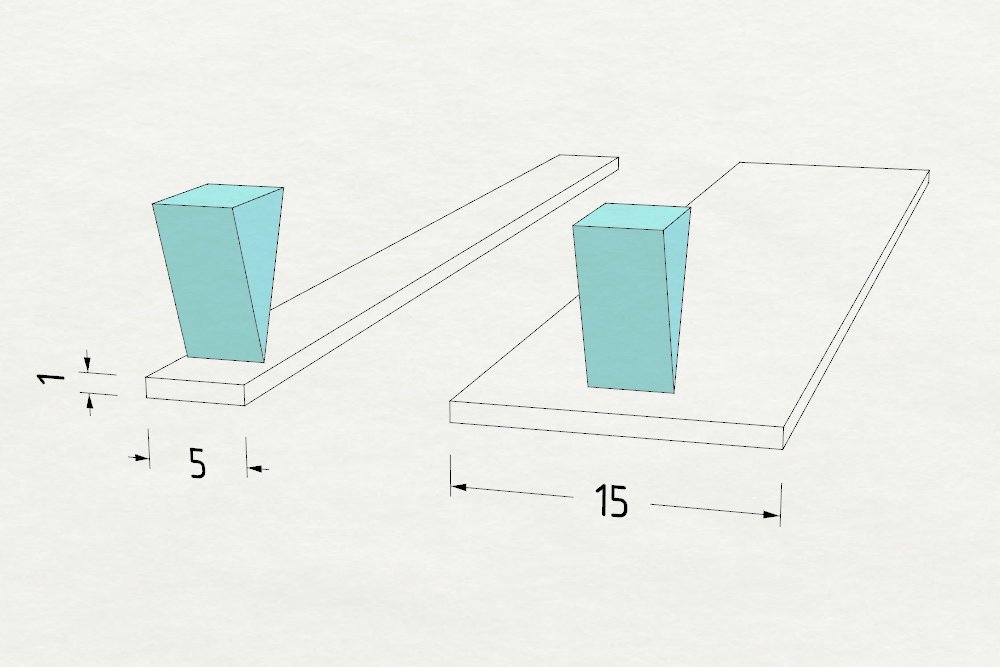
怎么辦到呢?我們試想另一個簡單的例子,假設你想修理一個機械連動裝置,這是大約1mm厚、5mm寬塑膠棒,X軸所承受的壓力持續毀損這根塑膠棒,你厘清這個問題之后,決定將壓力承受能力提升三倍。
我們最好怎樣達到目標呢?看一下 Fbreak 方程式,可見寬度(w)和最大承受壓力呈現線性關系,我們顯然要把橫木寬度從5mm加大為15mm,但反過來看,塑膠棒會變得太笨重,其重量和所需材料也會提升200%。
以天馬行空的方式,把零件的承壓能力提升三倍
當然還有更好的辦法。前述公式告訴我們,最大承受壓力跟高度(h)成正比,換言之,你只要把原本的高度加乘 √3,差不多是1.73mm,承壓能力就會提升三倍,所需材料卻只會增加73%,零件也很接近原本的形狀。
以更好的方法解決問題:增加零件的厚度
事實上,就連這個方法也太保守。若沒有理由保留原本的寬度,不妨把橫剖面變成正方形,讓X和Y的抗彎強度相等,這樣橫剖面會是2.47mm寬和2.47mm高,比起5mm x 1mm的橫木,這個所需材料只增加了22%,但承壓能力卻提升三倍。
不過先別急,還有一個問題:根據我們對彎曲壓力在橫木橫剖面分布的了解,大家不免懷疑舍棄中心附近的材料,難道不會犧牲整體抗彎強度嗎?我們試著打造一個工字梁,來看看實際成果如何吧。
為了搞清楚會有什么后果,我們不再關注長方形橫剖面的公式,反而要鎖定 Fbreak一般公式:
Fbreak = σmax * Ix / (L * cx)
既然工字梁是對稱的,中軸永遠都在中央,因此cx = h / 2。只有Ix
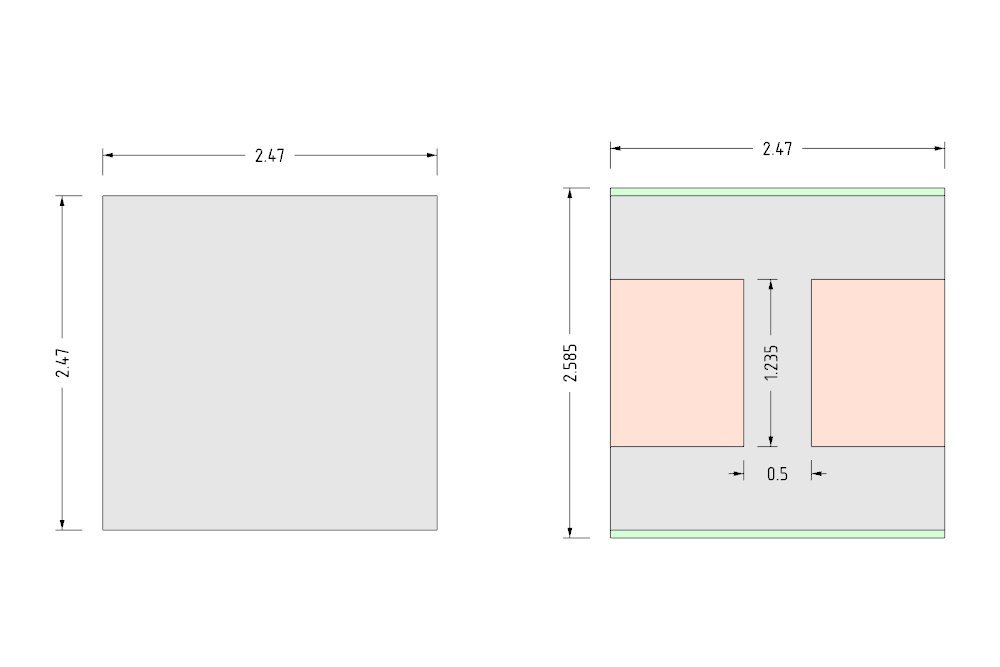
不知道數值,截面矩符號公式可在在線輕易找到,但這種橫木形狀有點麻煩,最好利用CAD軟件或在線計算器,得出移除中央材料后的Ix數值變化,才能知道外圍凸緣要增加多少,以便回復預計的Fbreak數值。
打造工字梁以符合預期目標。移除紅色區域,擠壓綠色區域。
上述例子從中央移除大量材料,外圍凸緣只要增加少數材料,橫木承壓能力就比5 x 1 mm增加了三倍…卻節省20%的材料,很棒吧?
事實上,工字梁在小型專題并不常見,主要是因為采用工字梁,反而會讓釘制過程變得更復雜(例如射出成型或金屬沖壓),但只要你觀察力夠好,你就會發現工業設計隨處可見其近親。
薄壁零件常見的強化方法,通道(右)也可能是圓形的
這些特征經常融入零件設計本身,舉凡肋材、巧妙彎曲的表面、有凸緣的蓋子等現代工業美學特色,這些絕對不是只為了好看,畢竟少了這些設計,我們的手機、整理箱和塑膠杯都可能馬上解體。
ATmega微控制器的AVR ISP MKII下載器,其注塑成型的外殼就包含強化后的肋材和特殊設計的墻面。(責任編輯:admin)





 3D打印太陽能塔或將成為月
3D打印太陽能塔或將成為月 如何干燥3D打印耗材:PLA
如何干燥3D打印耗材:PLA 什么是G代碼?
什么是G代碼? 關于3D打印中氧化鋯相關知
關于3D打印中氧化鋯相關知 Cura第一層設置:初始層
Cura第一層設置:初始層 一文了解3D打印水凝膠
一文了解3D打印水凝膠 6種從床上去除3D
6種從床上去除3D 2023年最佳免費3D
2023年最佳免費3D FDM耗材PLA與ABS
FDM耗材PLA與ABS 誰才是最好的模型
誰才是最好的模型 10種最常用的FDM
10種最常用的FDM 

